| accueil>techniques>aérodynamique>spp>2.2volplané | |
 | 2.2 Equilibre de vol plané | |
Malgré son titre, ce chapitre n'est pas réservé aux planeuristes. En effet, un avion dont le moteur a calé n'est rien de plus qu'un planeur. Le mot équilibre signifie pour un objet que sa vitesse dans l'espace est constante, à la fois en valeur et en direction. Une loi fondamentale de la mécanique nous dit que l'équilibre est atteint si et seulement si deux conditions sont vérifiées : - la somme vectorielle des forces appliquées à l'objet est nulle - la somme des moments des forces par rapport au centre de gravité de l'objet est nulle. Pour mémoire, le moment d'une force par rapport à un point est le produit de la valeur de la force par la distance séparant le point de la force. | ||
 |
 figure 20 | 2.2.1 Equilibre des forces | |
Tout çà est un peu pompeux, voyons l'application à un modèle planant ; la figure 20 montre un planeur en vol équilibré, et de plus en conditions standards, c'est à dire que l'axe longitudinal est parallèle à la vitesse. La résultante qui est la somme de la portance et de la traînée, équilibre exactement le poids. Mathématiquement, ceci s'écrit :  P : portance (N) T : traînée (N) b (>0) : pente de vol (degrés, °) M : masse du modèle (kg) g : accélération de la pesanteur (constante = 9,81 m/s2) Si les centres de gravité et de poussée sont bien confondus comme sur le dessin, la vitesse reste alors constante. L'équilibre est atteint. La direction du vol fait un certain angle avec l'horizontale : la pente de vol. Plus parlant que la pente, on préfère utiliser la "finesse". C'est le rapport de la distance horizontale parcourue sur l'altitude perdue. Exemple : en volant avec une finesse de 12, un planeur pourra parcourir horizontalement 120 m, avec une altitude de départ de seulement 10 m. La finesse se calcule facilement à partir de la pente de vol :  F : finesse (sans unité) b : pente de vol ( en degrés : °) Sur la figure 20, il est intéressant de remarquer que, dans ces conditions d'équilibre, l'angle que fait la portance avec la résultante est égal à l'angle de pente. Ceci nous permet d'écrire : 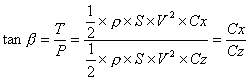 Ce qui nous donne, avec l'équation précédente :  F : finesse (sans unité) Cz : coefficient de portance du profil (sans unité) Cx : coefficient de traînée du profil (sans unité) La finesse est donc directement donnée par le rapport des coefficients de portance et de traînée du planeur. Elle représente en quelque sorte le rendement du modèle. La vitesse sur trajectoire peut aussi être calculée en fonction des Cz et Cx. Il suffit de réécrire l'équilibre des forces en remplaçant l'angle de pente par l'arctangente de Cx/Cz. On obtient après simplification : 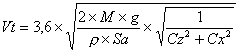 Vt : vitesse sur trajectoire (km/h) M : masse du modèle (kg) g : accélération de la pesanteur (9,81 m/s2) r : masse volumique de l'air (1,225 kg/m3) Sa : surface alaire (m2) Cz, Cx (sans unité) Le facteur 3,6 donne un résultat en km/h, plutôt qu'en m/s. La vitesse horizontale et le taux de chute s'obtiennent alors en faisant :  Vt : vitesse sur trajectoire (km/h) Vh : vitesse horizontale (km/h) Vz : taux de chute (km/h) | ||
|
 figure 21 | 2.2.2 Equilibre des moments | |
Nous venons de voir ce qu'implique l'équilibre des forces lors du vol plané. Ces calculs de performances, faits à partir des valeurs de Cz et Cx du planeur complet, vous permettront de choisir l'angle d'incidence du profil d'aile correspondant le mieux à ce que vous souhaitez obtenir comme vol standard. La deuxième condition pour que le planeur conserve sa trajectoire réside dans l'équilibre des moments au centre de gravité CG, comme mentionné plus haut. Deux forces sont susceptibles d'avoir un moment par rapport au CG : - la portance de l'aile, - et la portance de stab. Pour que l'équilibre ait lieu, il faut donc avoir :  MPa : moment de la portance de l'aile par rapport au centre de gravité (Newton mètre, Nm) MPs : moment de la portance du stab par rapport au centre de gravité (Nm) La figure 21 montre une situation où ceci est vérifié. On peut s'amuser à développer cette équation pour aboutir à une relation liant distance CP-CG et Cz de stab. La manière la plus simple de la résoudre reste quand même de vérifier :  Le moment d'une force par rapport à un point est nul dans des cas divers, dont font partie les deux suivants : - la force est nulle, ou bien - la distance entre son point d'application et le point de référence est nulle. Ici, nous aurons un de ces cas : - pour le moment de stab, c'est la portance qui sera égale à zéro, et - pour l'aile, c'est la distance du centre de poussée au centre de gravité qui sera inexistante : CP et CG seront confondus. Le modèle devra donc être centré exactement au centre de poussée, et son stab calé de manière à ce qu'il ne porte pas du tout en vol standard. Il est à remarquer que cette solution simple est aussi la plus performante : en effet, c'est à portance nulle que le stab traînera le moins. | ||
|
bientôt sur les pistes pour de bons vols ...
agrandissement